Linear regression is known as a least squares method of examining data for trends. As the name implies, it is used to find “linear” relationships. To begin our discussion, let’s turn back to the “sum of squares”:

, where each x_i is a data point for variable x, with a total of n data points.

The sum of squares is used in a variety of ways. One common way is in the calculation of variance, which is a measure of the variability in a dataset (though a different term also called variance is used to measure uncertainty – we will not be dealing with this other term here):

.

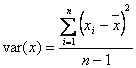Note that this equation looks very similar to the equation for the mean, given as:

.

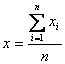The only major difference is that instead of taking the mean of the data points, we’re taking the mean of the squared distances between the data points and their mean. (Note: The n-1 term in the denominator of the variance is due to bias in estimation that occurs due to sample size, and its explanation is beyond the scope of this course). Please note, also, that the standard deviation of a dataset is just the square root of the variance.

Another common way that the sum of squares is used is in the calculation of covariance. The covariance is calculated from a form of the sum of squares called the “sum of cross-products”. This term is calculated using two variables, and is given as the following:

.

This term is very similar to the sum of squares, but it looks at the relationship between two variables. We use this term when we have data pairs, or coordinates ((x₁, y₁),(x₂,y₂)…), and wish to examine whether a relationship exists between the two. We take the x term in one set of coordinates, subtract the mean of x from it, and multiply the difference by the analogous difference in the y term. Since there are n coordinates, we sum the n cross-products together.

The covariance is just the mean cross-product, given as:

.

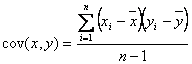This term is exactly analogous to the variance term, only it deals with two variables and their relationship, rather than just one variable. One other interesting difference is that the covariance term may be negative.

One major property of sum of squares and sum of cross-products that is useful to biologists is inherent in the name. In both cases, we are dealing with sums. In other words, variance and covariance may be treated as additive. Hence, we can divide up the variance by meaningful biological categories, such as variance due to inheritance, environment, etc.

Back to Regression

To ascertain whether there is a linear, dependent relationship between two variables, we first need a data set to work from. In this data set, data are paired. That is, one value of x is associated with one value of y. One variable must also be independent of the other, while the other variable must be directly or indirectly dependent on the other (though this can be tested with regression). As an example, we may work with heights of parents and their children. In this case, children’s heights are dependent on their parents’ heights, but not vice versa. So, parental height is the independent variable, or x, while offspring height is the dependent variable, or y.

Next, we need to estimate a line. A line is given by the following equation:

.

Here, a is the y-intercept and b is the slope. To calculate b, we use the following equation:

.

Remember that the slope is the change in the dependent variable divided by the change in the independent variable. Here, we are dealing with variation in data rather than absolute differences between coordinates. That is because we cannot expect nature to produce perfect linear relationships for us, nor can we so accurately measure variables that no error enters into the data set. Hence, we are defining the slope as the proportion of the variance in the independent variable that covaries with the dependent variable. This is the slope of the linear relationship hidden within the cloud of data we have. As it happens, if our data actually look like a circular cloud when we plot them, our slope will become 0, suggesting no causal relationship between variation in x and y.

To solve for the y-intercept, we use the following equation:

.

Easy as cheese.

Next, we are interested in determining the proportion of the variability in y that is explained by variability in x. This is called the coefficient of determination, r², and it is different from calculating the slope. Instead, this tests how closely around the predicted line the data cluster, assuming that there is a relationship to begin with (i.e., slope is not 0). To do this, we calculate:

.

If this term equals 1, then y is completely predictable from x, and all of the variation we see in the dependent variable is explained by associated variability in the independent variable. For an ecologist, this situation would be a dream come true! If this term is 0, then none of the variation in y is explainable by x.

Okay. That’s enough of my babbling for now. Here’s an assignment:

1. Look at the following data set. BY HAND, estimate the linear equation between child height and parent height (both are given in cm), and calculate the coefficient of determination, as well. Make sure you assign the proper variables as dependent and independent!

Parent Ht	Child Ht
166	157
183	174
178	168
180	181
168	169
171	176
173	165
178	169
172	179
177	174

2. Now let’s try something a little more challenging. Let’s do this with the help of Excel. To use Excel’s statistical features, click on the Tools menu and choose Add-Ins. Then, make sure the Analysis Toolpak box is checked. Then, enter the following data into two columns in Excel. Finally, click on Tools, and then Data Analysis. Choose Regression from the list. Under “Input Y Range”, enter the range of the dependent data. You may also highlight the appropriate boxes (to do this, click on the little red arrow next to the input box and Excel will let you go to the spreadsheet to highlight the right selection). Next, choose the independent variable. Click OK. Can you interpret the results? What is the y-intercept? What is the slope? These are given under the column “Coefficients” in the bottom box. What is the estimated coefficient of determination? This is given in the row “R squared” in the top box. Print out the results of Excel’s analysis, write down the equation of the line on that page, and interpret all of the results that you can interpret.

Parent Ht	Child Ht
64.9	61.36
71.31	68.14
69.46	65.43
70.31	70.75
65.48	66.02
66.63	68.71
67.63	64.46
69.68	66.04
67.13	70.01
68.97	67.84
72.89	71.96
71.62	74.05
71.99	71.76
70.73	66.43
66.86	69.71
64.37	64.18
69.16	74.58
68.84	64.63
68.02	63.96
68.93	63.91
68.53	64
67.04	71.12
69.92	66.64
69.28	66.49
69.91	66.36
68.43	70.54
68.23	69.93
68.52	69.92
68.58	69.49
68.08	69.44

3. Now try flipping the variables around. Take the variable you logically inferred to be the dependent variable in the previous question, and treat it as the independent variable in a new analysis. Likewise, treat the old independent variable as the new dependent variable. What do you predict will happen to the slope, y-intercept, and coefficient of determination?

Note: The data used for these problems actually comes from Francis Galton’s data on human height. Be careful that you don’t make the same misinterpretations that he did!