Key to Quizzes for 9 and 10 October 2002-10-12
Wednesday Quiz:
Question:† In a human population of 200 people, 17 had type A blood, 52 had type B blood, 3 had type AB blood, and 128 had type O blood.† Assuming the population is in Hardy-Weinberg equilibrium, what are the allele frequencies?
Given:† Type A is dominant to type O.† Type B is dominant to type O.† Types A and B are co-dominant to each other.† Type O is fully recessive.
Solution:
Type A blood comes about through two different genotypes: AA and AO.† Type B comes about also through two different genotypes: BB and BO.† Notice that this is due to the dominance of the A and B alleles to the O allele.† So, these phenotypes are due to both homozygous and heterozygous conditions.† However, type AB only comes about through one genotype: AB.† This is a heterozygous condition.† Lastly, type O also comes about only through one genotype: OO.† This is a homozygous condition.
We are assuming Hardy-Weinberg equilibrium.† So, with three alleles, the genotypic frequencies must look like this:
p2 + 2pq + q2 + 2pr + r2 + 2qr = 1
where p = allele frequency of A, q = allele frequency of B, and r = allele frequency of O.† This equation has every combination of two alleles possible Ė all homozygotes and heterozygotes that can be produced, are produced, and in Hardy-Weinberg proportions.† If the population size is N, then we also know that:
N ( p2 + 2pr
) = the number of type A people in the population,
N ( q2 + 2qr
) = the number of type B people in the population,
N ( 2pq ) =
the number of type AB people in the population, and
N ( r2 ) = the number of type O people in the population.
Notice that we fit both homozygote and heterozygote frequencies into the type A and type B equation.† However, the type AB and type O equations are only due to either heterozygotes or homozygotes.† That makes them much simpler.
We want to solve for p, q, and r, so letís take the simplest equation, the type O equation, which has only one variable to solve for:
N ( r2 ) = 128 = 200 * r2
r2 = 128 / 200 = 0.64
r = √ ( r2 ) = √ (0.64) = 0.8
So, we now know the allele frequency for the allele O.† Next, we can choose to tackle either the A allele frequency or the B allele frequency.† Letís try the A allele:
N ( p2 + 2pr ) = 17 = 200 ( p2 + 2pr )
p2 + 2pr = 17 / 200
p2 + 2pr = 0.085
p2 + 2p(0.8) = 0.085
p2 + 1.6 p = 0.085
p2 + 1.6 p - 0.085 = 0
So, we have a quadratic equation that solves for p.† Do you remember the quadratic equation?† If the quadratic formula is ax2 + bx + c = 0, then the quadratic formula is given as:
![]()
Letís use this equation to solve for p.
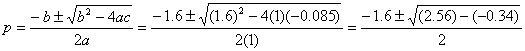
![]()
So, we have two solutions for p.† Since p cannot be negative, we know that p = 0.0515.† Weíve now solved for p and r.† How do we solve for q?† Very simply!† We solve the following equation for q:
p + q + r = 1
q = 1 - ( p + r )
q = 1 - ( 0.0515 + 0.8 )
q = 1 - ( 0.8515 ) = 0.1485
Thursday Quiz:
Question:† Shell color in the European snail is controlled by three alleles at a single locus: CB (brown), CP (pink), and CY (yellow).† The brown allele is dominant to both pink and yellow; pink is dominant to yellow; yellow is completely recessive.† In one population of snails the colors are distributed as follows:
Brown:† †††††††††† 472
Pink:†††††††††††††††† 462
Yellow: 66
TOTAL:†††††††††† 1000
If this population is in Hardy-Weinberg equilibrium, what are the allele frequencies?
Solution:†
We use the same strategy for this problem as in the Wednesday quiz problem.† That means that all the genotypes fit together in the population along the lines of the following equation, the Hardy-Weinberg equilibrium for three alleles:
p2 + 2pq + q2 + 2pr + r2 + 2qr = 1
where p = allele frequency of CB, q = allele frequency of CP, and r = allele frequency of CY.† This equation has every combination of two alleles possible Ė all homozygotes and heterozygotes that can be produced, are produced, and in Hardy-Weinberg proportions.† If the population size is N, then we also know that:
N ( p2 + 2pq
+ 2pr ) = the number of brown snails in the population,
N ( q2 + 2qr
) = the number of pink snails in the population,
N ( r2 ) = the number of yellow snails in the population.
We want to solve for p, q, and r, so letís take the simplest equation, the yellow snail equation, which has only one variable to solve for:
N ( r2 ) = 66 = 1000 * r2
r2 = 66 / 1000 = 0.066
r = √ ( r2 ) = √ (0.066) = 0.257
Letís tackle the next easiest equation, that for pink snails, next:
N ( q2 + 2qr ) = 1000 ( q2 + 2qr ) = 462
q2 + 2qr = 462 / 1000 = 0.462
q2 + 2q(0.257) = 0.462
q2 + 0.514q - 0.462 = 0
Once again, we plug these numbers into the quadratic equation.† As I showed how to do this in the previous problemís key, Iíll just give you the answer:
q = 0.470
Once again, p + q + r = 1, so p = 1 Ė (0.470 + 0.257) = 0.273