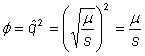How does mutation affect evolution?
Model
Start with chalcone synthetase locus
Wildtype allele A1 codes for blue flowers
Suppose that A2 is a mutant allele at this locus
Produces an ineffective enzyme that cannot produce pigment
A loss of function that codes for white flowers
Initial allele frequencies
p = freq(A) allele
q = freq(a) allele
Stipulate symbols for mutation rates
Let m = rate/generation at which A mutates to a
And n = rate/generation at which a mutates back to A
Assume that mutations occur while gametes are in gamete pool (after shedding, before fusion)
So, gametes enter gamete pool in frequencies of p and q
But then allele frequencies are altered by mutation
Frequency of forward mutations
Frequency of A gametes in
population times rate at which they can mutate to a = pm
Frequency of backward mutations
Frequency of a gametes in population times rate at which they can mutate to A = qn
Hence,
Frequency of A gametes after mutation events
p* = p - mp + nq
Frequency of a gametes after mutation events
q* = q + mp - nq
Note
p* + q* = p - mp + nq + q + mp - nq = p + q = 1
Calculate genotype frequencies for next generation (assume H-W equilibrium)
Freq(AA) = (p*)2 = (p - mp + nq )2
Freq(Aa) = 2(p*q*) = 2(p - mp + nq )(q + mp - nq)
Freq(aa) = (q*)2 = (q + mp - nq)2
Calculate rate of change of frequencies
Dp = p* - p = (p - mp + nq ) – p = nq - mp
Dq = q* - q = (q + mp - nq) – q = mp - nq
Is mutation an important evolutionary force?
What would rate of evolution be if only evolutionary forces was mutation?
Suppose that new mutation arises
In a population fixed for A , new allele a arises by new mutation
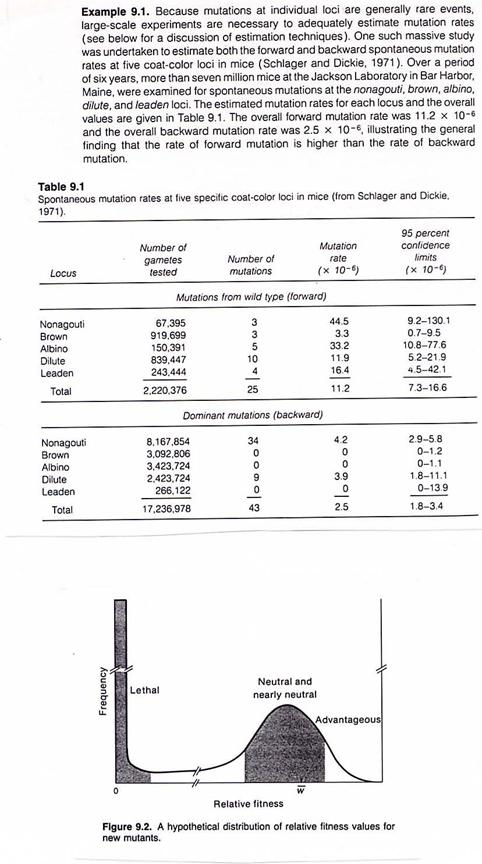
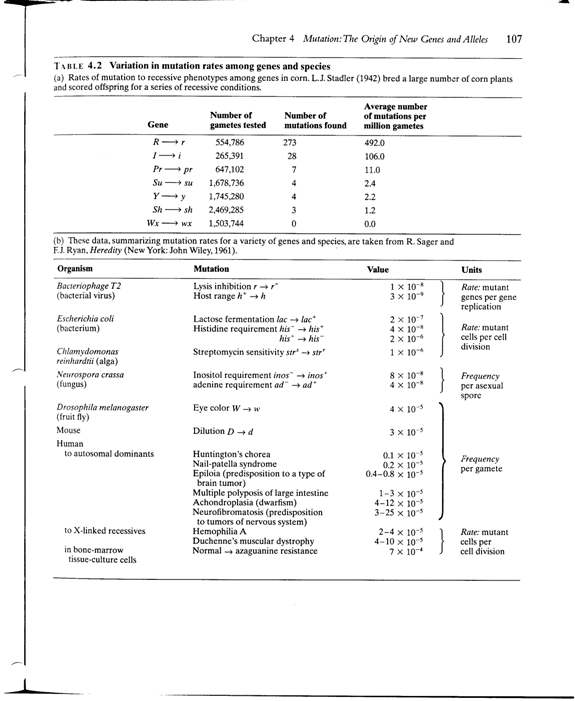
Mutation rate (A®a) is 11.2 x 10-6 = m
Back-mutation rate (a®A) is 2.5 x 10-6 = n
Then,
Dp = p* - p = (p - mp + nq ) – p = nq - mp = 2.5 x 10-6 (0) – 11.2 x 10-6 (1) = -11.2 x 10-6
Dq = q* - q = (q + mp - nq) – q = mp - nq = 11.2 x 10-6 (1) – 2.5 x 10-6 (0) = 11.2 x 10-6
Ignore back-mutation
Dp = p* - p = -mp
Dq = q* - q = mp
Extra points on mutation as evolutionary force:
Can derive more general equation if we assume that family size follows a Poisson distribution with mean family size = k
I’m not prepared to derive this equation,
and don’t expect you to be able to do so
But, if you understand probability
distributions, you could do so
Where x1
= probability mutation will persist to 2nd generation
k = average family size when family size follows a
Poisson distribution
When average family size (k = 2), then
Also, don’t expect you to be able to use
this equation
Approximately 36.8% of time, new mutant will
be lost in one generation
As family size increases, this probability decreases
So, more chance of mutant persisting in population
Selection is major force that prevents detrimental alleles from increasing in frequency
Modeling mutation-selection balance
First, assume that mutant is deleterious recessive
Selection against deleterious recessive
Increase in frequency due to mutation
Because selection and mutation are opposing forces, they balance each other to create an equilibrium
So, at some point,
Or, 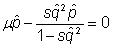 ,
, 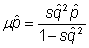
If we assume that the mutant is rare, then q2 is very small and denominator of right side of the equation can be treated as unity
Then, cancel p from each side to get 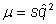
And, equilibrium allele frequency is
Second, assume that mutant is deleterious dominant
Selection against deleterious dominant
Increase in frequency due to mutation
Because selection and mutation are opposing forces, they balance each other to create an equilibrium
Or, 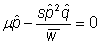 ,
, 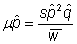
If we assume that the mutant is rare, then q2 is very small and all term with q2 go to zero
Also, if mutant is rare, then qm is vanishingly small
And equilibrium allele frequency is
Think about the form of this equation
Again, when selection is strong and mutation rate is low, equilibrium frequency of mutant allele is low
Apply these equations to the delphiniums studied by Nick Waser and Mary Price
Observed average frequency of albino plants = 7.4 x 10-4
i.e. less than one albino plant per thousand individuals
Assumed that this is the equilibrium phenotype frequency
Also measured selection against albinos by pollinators
Found that albinos produced from 20% (in artificial populations) to 70% (in natural populations) the number of seed found on blue-flowered wildtypes
So, s = 0.3 to 0.8
Next calculated expected equilibrium phenotype frequency at mutation-selection equilibrium
First, assumed that albinism is due to a single gene with a recessive white mutant allele
So, assumed white-flowered plants are aa homozygous mutants
Calculated equilibrium phenotype frequency by assuming selection against recessive homozygous mutant (equations above)
Designated frequency of mutant allele (a) = q
Assumed H-W equilibrium
Frequency of mutant homozygote = q2
Hence, equilibrium phenotype frequency at mutation selection balance = 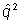
Plug in observed values
Low range of selection
High range of selection
Second, assumed that albinism is due to a single gene with a partly or completely dominant white mutant allele
So, assumed white-flowered plants are either homozygous (aa) or heterozygous (Aa)
Calculated equilibrium phenotype frequency by assuming selection against dominant or co-dominant mutant
Designated frequency of mutant allele (A) = q
Important assumptions
Assumed H-W equilibrium
Frequency of the mutant
phenotype = 2pq
Mutant phenotype class
probably consists of only heterozygotes
Because the rarity of the
mutant ensures a low frequency of homozygous mutants
And because the dominant
homozygotes is probably lethal