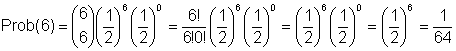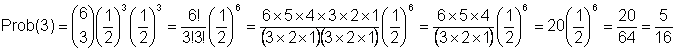Modeling drift over one generation of bottleneck

Our hypothetical example (from tussock moths after lupines die)

Parental population

With

Frequency of F alleles = p = 0.5

Frequency of S alleles = q = 0.5

Release gametes into gamete pool

Gamete frequencies

Same as parentals (no selection)

Frequency of F alleles = p = 0.5

Frequency of S alleles = q = 0.5

Assume that only N = 3 zygotes survive

Generate these 3 zygotes by sampling 2N gametes from the gamete pool

First, think of drift as a process of sampling gametes

What happens to allele frequencies?

In a diploid organism

Sampling gametes from gamete pool is a binomial process

Because there are only two possible outcomes to each trial

Either gamete will have F allele or it will have S allele

Binomial sampling process modeled by binomial probability

Remember binomial theorem from your homework assignment?

Binomial theorem states

Where

n = number of events = 2N gametes sampled

s = number of times a gamete has an F allele

(n-s) = t = number of times a gamete does not have an F allele

(and instead has an S allele)

For example,

What is probability that population will fix for F allele after this bottleneck down to a population of 3 caterpillars?

= Probability that all 3 zygotes will be homozygous FF

= Probability that all (2 x 3 = 6 gametes) will have F alleles

So,

n = number of events = 2N gametes sampled = 6

s = number of times a gamete has an F allele = 6

(n-s) = t = number of times a gamete does not have an F allele = 0

(and instead has an S allele)

A second example,

What is probability of obtaining one of each genotype?

= Probability that the three zygotes are (FF, FS, SS)

= Probability that 3 gametes have F allele and 3 gametes have S allele

So,

n = number of events = 2N gametes sampled = 6

s = number of times a gamete has an F allele = 3

(n-s) = t = number of times a gamete does not have an F allele = 3

(and instead has an S allele)

Now, think of drift as a process of sampling zygotes

What happens to allele frequencies?

In a diploid organism

Sampling zygotes from zygote pool is a trinomial process

Because there are three possible outcomes to each trial

Either a zygote will have FF genotype or it will have FS genotype or SS genotype

Trinomial sampling process modeled by trinomial probability

Trinomial theorem states

Where

n = number of events = N zygotes sampled

s = number of times a zygote has an FF genotype

t = number of times a zygote has an FS genotype

n-(s+t) = u = number of times a zygote does not have an FF or FS genotype

(and instead has an SS genotype)

Assume HW equilibrium

P = frequency of FF genotype

P = p²

H = frequency of FS genotype

H = 2pq

Q = frequency of SS genotype

Q = q²

For example,

What is probability that population will fix for F allele after this bottleneck down to a population of 3 caterpillars?

= Probability that all 3 zygotes will be homozygous FF

So,

n = number of events = N zygotes sampled = 3

s = number of times a zygote has an FF genotype= 3

t = number of times a zygote has an FS genotype = 0

n - (s+t) = u = number of times a zygote does not have either an FF or an FS genotype = 0

(and instead has an SS genotype)

Again, assume HW equilibrium

P = frequency of FF genotype

P = p²

H = frequency of FS genotype

H = 2pq

Q = frequency of SS genotype

Q = q²

A second example,

What is probability of obtaining one of each genotype?

= Probability that the three zygotes are (FF, FS, SS)

So,

n = number of events = N zygotes sampled = 3

s = number of times a zygote has an FF genotype= 1

t = number of times a zygote has an FS genotype = 1

n - (s+t) = u = number of times a zygote does not have either an FF or an FS genotype = 1

(and instead has an SS genotype)

Again, assume HW equilibrium

P = frequency of FF genotype

P = p²

H = frequency of FS genotype

H = 2pq

Q = frequency of SS genotype

Q = q²

Why is this result different from the one obtained by sampling gametes?

Because can get 3 F alleles and 3 S alleles in more ways than simply FF FS SS

Can also be from FS FS FS

A final example,

What is probability that our sample if 3 caterpillars will all be heterozygotes?

= Probability that all 3 zygotes will be homozygous FS

So,

n = number of events = N zygotes sampled = 3

s = number of times a zygote has an FF genotype= 0

t = number of times a zygote has an FS genotype = 3

n - (s+t) = u = number of times a zygote does not have either an FF or an FS genotype = 0

(and instead has an SS genotype)

Again, assume HW equilibrium

P = frequency of FF genotype

P = p²

H = frequency of FS genotype

H = 2pq

Q = frequency of SS genotype

Q = q²

Thus, probability of offspring generation having 6 S and 6 F alleles

= prob(FS, FS, FS) + prob(FF, FS, SS) = 3/16 + 2/16 = 5/16

Same result as obtained from gamete sampling!

What have we observed?

Sampling a small number of individuals (or gametes to produce those individuals) can change allele frequencies entirely by chance

Thus, small populations can violate HW equilibrium even though individuals are randomly mating and are experiencing no selection

It is not possible to predict the allele frequency of a population after drift

Can only predict the probability with which any particular frequency will be obtained

Over many generations, sampling errors average out

Eventually one allele or the other can fix

The probability of fixation is determined by the allele frequency at the start of the drift process

Thus, drift erodes genetic diversity

General rules about genetic drift